Bubble Sort

---

Bubble Sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order.
The pass through the list is repeated until the list is sorted.
It is called Bubble Sort because smaller elements "bubble" to the top of the list with each pass.

---

function bubbleSort(arr) {
    var n = arr.length;
    var swapped;
    do {
        swapped = false;
        for (var i = 0; i < n - 1; i++) {
            if (arr[i] > arr[i + 1]) {
                // Swap arr[i] and arr[i + 1]
                var temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
                swapped = true;
            }
        }
    } while (swapped);
    return arr;
}

var array = [64, 34, 25, 12, 22, 11, 90];
console.log("Original array: " + array);
console.log("Sorted array: " + bubbleSort(array));

---

Time Complexity:
Worst Case: O(n^2)
The worst case scenario occurs when the input array is sorted in reverse order. In this case, Bubble Sort performs n passes through the array, and in each pass, it makes a swap for each pair of adjacent elements. This results in a time complexity of O(n^2).
Space Complexity:
Bubble Sort is an in-place sorting algorithm, meaning it does not require additional space proportional to the input size.
It sorts the elements within the given array itself, so the space complexity is O(1), indicating constant space usage regardless of the input size.

---

Refereneces:
https://s-satsangi.medium.com/insertion-sort-selection-sort-and-bubble-sort-5eb16d55a4de

Read More

Quick Sort

 Quick Sort

Quick Sort is a sorting algorithm first proposed by Charles Antony Richard Hoare in 1960, and since then, many people have modified and improved it. 

Even after more than half a century since its introduction, Quick Sort remains one of the fastest sorting algorithms in existence. 

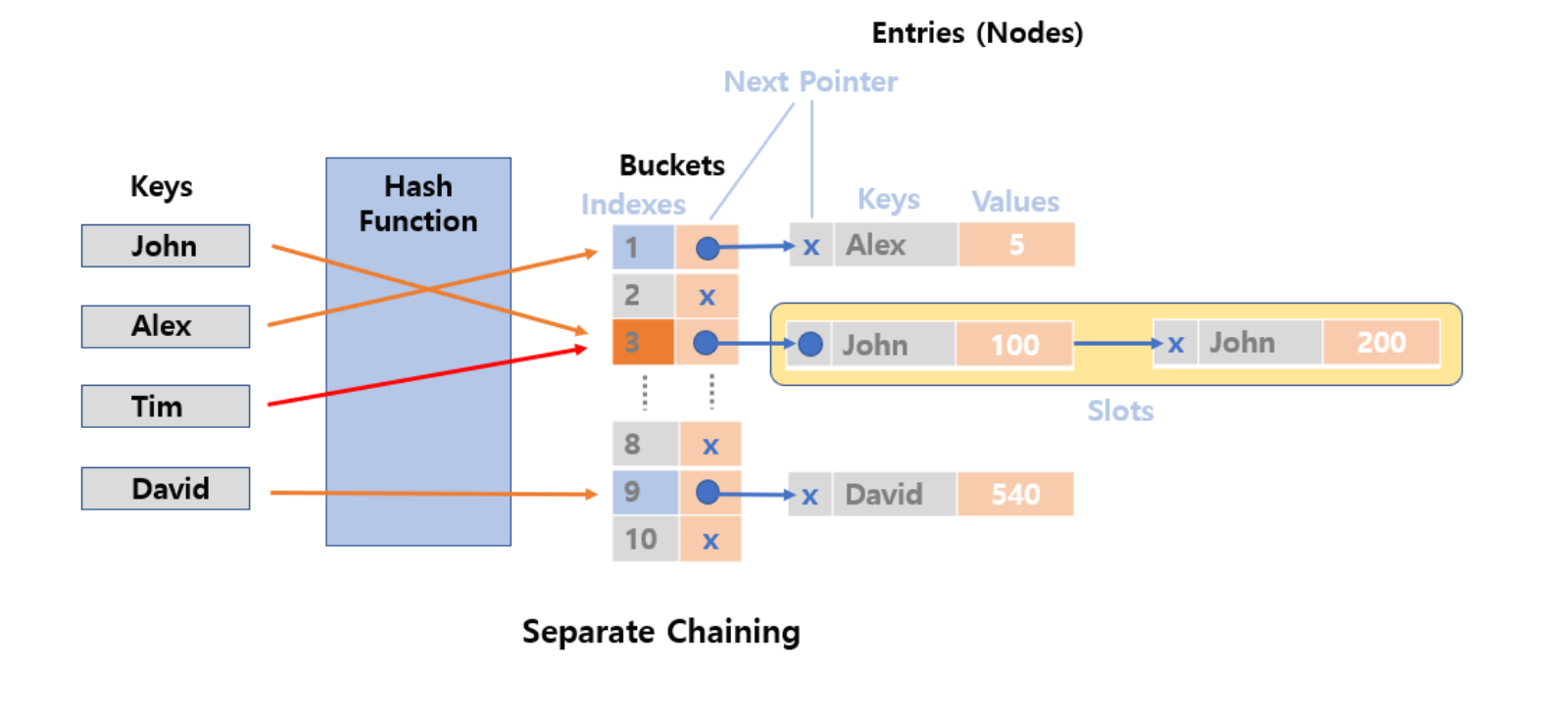
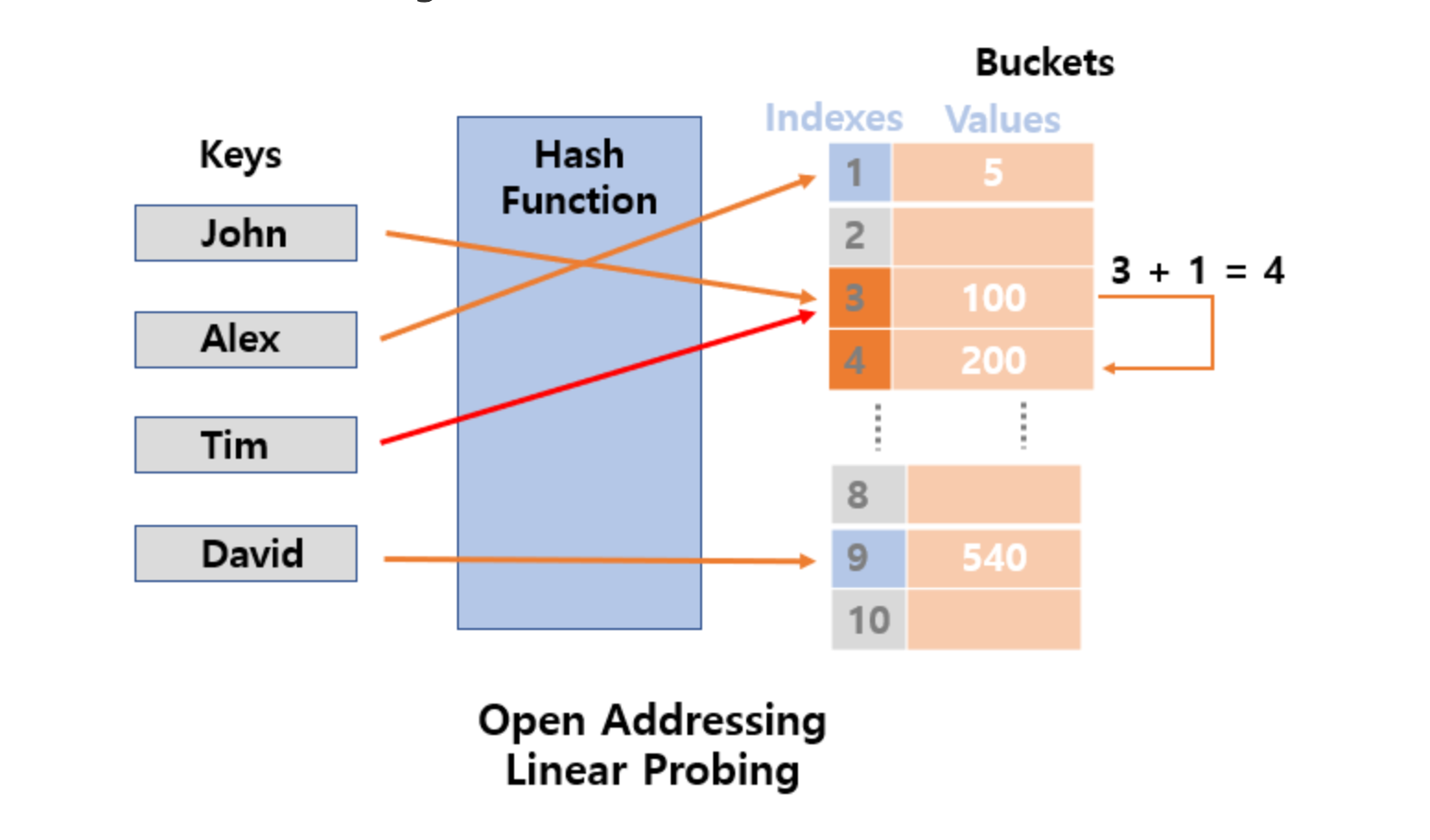
There are two types of Quick Sort: in-place and not in-place. 

The in-place method, which uses less memory, is the most commonly used. 

However, the not in-place method is easier to understand intuitively, so we will explain that first, followed by the in-place method

graphical representation:

1. Choose a pivot element. In this example, we've chosen the first element of the array as the pivot.
2. Partition the array into two sub-arrays: one containing elements smaller than the pivot, and one containing elements greater than the pivot.
3. Recursively apply the quicksort algorithm to the sub-arrays.

The above method of quicksort is not an in-place method and requires additional memory space. Therefore, it may not be a practical solution for sorting large datasets due to the potential for significant memory waste.

However, using this method, we can achieve a stable sort where the order of duplicate elements remains unchanged since duplicate elements are sequentially placed on the pivot element during the sorting process.

Merge Sort: 

Merge sort is a stable sorting algorithm that belongs to the category of divide and conquer algorithms, which was proposed by John von Neumann. 

Divide and conquer is a problem-solving strategy that involves dividing a problem into smaller sub-problems, solving each sub-problem, and combining the solutions to solve the original problem. 

The divide and conquer approach is often implemented using recursive function calls.
The merge sort algorithm works by dividing an unsorted list into two equal-sized sublists, sorting each sublist recursively using merge sort, and then merging the sorted sublists to create a sorted list.

The merge sort algorithm involves the following steps: Divide the input array into two equal-sized subarrays; Sort each subarray recursively using merge sort; Merge the two sorted subarrays to create a single sorted array.

Merge sort requires additional memory for merging the subarrays, but it provides a stable sort and guarantees a worst-case time complexity of O(n log n).

 

Quick Sort:

• Sorts an array by dividing it into two sub-arrays based on the pivot value.
• If the size of the sub-array is small enough, it is sorted directly. Otherwise, the process is repeated recursively.
• The position of each pivot is guaranteed to be fixed after each sort, ensuring that the sorting process will eventually end.
• The choice of pivot can be optimized to improve the efficiency.

Merge Sort:

• Sorts an array by dividing it into two sub-arrays, sorting them recursively if necessary, and then merging them into one list.
• Merge sort is a stable sorting algorithm, while Quick Sort is not.
• The time complexity of both algorithms is O(n log n), but the worst case time complexity of Quick Sort is O(n^2).
• Merge Sort requires additional memory space for the merging process.

Common features:

• Both algorithms are based on the divide and conquer strategy.
• Both algorithms are generally faster than other sorting algorithms.

 

 

 

Read More

Hash table

What is Hashtable? 

A Hashtable is a data structure that stores key-value pairs, allowing for efficient access and retrieval of values based on their associated keys.

In a Hashtable, the key is used to calculate an index into an array of buckets, which contain the values.

Since the value being searched for and the index of the table are the same, it is possible to directly access the location where the value is stored without having to search through the table. Therefore, the time complexity is O(1).

Similarly, actions such as inserting, modifying, and deleting values in the table can also be resolved in O(1) time complexity as long as the location of the value is known. The reason why algorithms for searching, inserting, modifying, and deleting values in such simple data structures usually take up time is often quite similar.

Advantages of Hashtable:

• Fast access: Hashtable allows for fast access to values based on their keys.
• Efficient storage: Hashtable typically uses less memory than other data structures, such as linked lists or arrays, for storing large amounts of data.
• Flexibility: Hashtable is a dynamic data structure that can grow or shrink as needed.

Disadvantages of Hashtable:

• Hash collisions: If two keys map to the same index in the array, a hash collision occurs, which can reduce the efficiency of the Hashtable.
• No ordering: Hashtable does not maintain the order of the inserted elements, making it unsuitable for some use cases.
• Additional memory: Hashtable requires additional memory to store the array of buckets.

Use Cases:

• Caching: Hashtable can be used for caching frequently accessed data to improve performance.
• Dictionary: Hashtable can be used as a dictionary, with words as keys and definitions as values.
• Counting occurrences: Hashtable can be used to count the occurrences of items in a dataset.

Collision:

When a different value is inputted into the hash function, but the same value pops out, it is called a collision.

deleting values in such simple data structures usually take up time is often quite similar.

 

Hash tables, which are made up of keys and values, are a data structure that exhibits excellent performance. However, they cannot be used in all cases due to hash collisions. 

Hash collisions occur when different keys result in the same hash code through a hash function. 

In hash tables, the problem caused by collisions is solved by two methods: separate chaining and open addressing.

Separate Chaining:

 

Separate Chaining is one of the methods for resolving collisions in hash tables, which manages data stored in the same bucket by linking them with a linked list. 

When accessing the same bucket, it searches for data by following the linked list, as shown in the diagram.

Chaining method has the advantage of not requiring expansion of the hash table, being simple to implement, and being easy to delete data. 

However, the disadvantage is that as the number of data increases, the efficiency of the cache decreases as more data is linked to the same bucket with a linked list.

 

Advantages:

Efficient use of limited buckets. No need to allocate space in advance, reducing memory usage. Use of linked lists reduces constraints on the amount of data that can be added.

Disadvantages:

Reduced search efficiency when multiple keys have the same hash and multiple items are in one bucket. Additional memory is required to use linked lists. In the worst case, all nodes can be inserted into the same bucket.

Time complexity:

 Worst case- O(n) A linked list of length n can be created if all keys are hashed to one slot. Average performance: O(1+α) (α = Load factor) It takes O(1) time to access the table slot, and O(α) time to search the list in that slot.

Open Addressing:

Open Addressing is a method that utilizes the empty spaces in a hash table, unlike the Chaining method that uses additional memory such as linked lists. Therefore, it takes up less memory than the Separate Chaining method.

In a hash table, one hash and one value are maintained to match. 

When a collision occurs in a bucket, the index is changed, and the hash is stored in a different bucket.

There are three main methods for implementing Open Addressing.

 

1. Linear Probing

When a collision occurs, search for the next available bucket by moving a fixed distance from the current bucket index and store the data in the first available bucket found.

 

Advantages: Easy to implement.

Disadvantages: Primary clustering problem Clustering is a phenomenon where groups of consecutive data are formed, and it can degrade hashing efficiency by taking longer search time.

The search interval can be set to a value other than 1, but it should be chosen as a prime number that is relatively prime to the table size to reduce the clustering phenomenon.

Also suffers from secondary clustering problem which can occur when a probing sequence hits an already occupied slot, resulting in another probing sequence starting from that position.

 

2. Quadratic Probing 

This method stores the hash sequence widths as squares. 

For example, if a collision occurs for the first time, the data is stored by moving one position, and if subsequent collisions continue to occur, the data is stored by moving two, four, and so on positions according to the square of the sequence number.

 

Advantages:

• Less clustering than linear probing.

Disadvantages:

• Secondary clustering problem. If the initial probe value of two keys is the same, the process of finding an empty slot will be the same, leading to searching the same slot repeatedly at the next collision position.

 
3. Double Probing is a method of eliminating the regularity of hashing by hashing the hashed value once more and assigning a new address. Because the hashed value is hashed again to assign a new address, it requires more operations than other methods.

Advantages:

• Less clustering compared to linear probing.

Disadvantages:

• Secondary clustering problem: If the initial probe values of two keys are the same, they will search for the same slot because they follow the same process of finding an empty slot. Therefore, they will continue to collide repeatedly at the same position as they did initially.
• When deleting data in open addressing, the deleted space is utilized as a dummy space, and reorganization of the hash table is required.
• The load factor in open addressing is less than or equal to 1 because the array size is limited.
• The computational complexity in open addressing is proportional to the number of probes, so the time complexity can be represented by the number of search probes.
• For linear probing, the time complexity is as follows: successful search - 1/2 * 1 + 1/(1-α), unsuccessful search - 1/2 * 1 + 1/(1-α)^2. If the load factor exceeds 0.5 in linear probing, the number of unsuccessful searches increases dramatically, so it is necessary to increase the size of the hash table to maintain a load factor of less than 0.5.
• It is recommended to maintain a load factor of less than 0.5 in quadratic probing and double hashing.

References: 

• https://www.geeksforgeeks.org/java-util-hashtable-class-java/

• https://www.tutorialspoint.com/python_data_structure/python_hash_table.htm

• https://developer.ibm.com/articles/cc-hashtablesincsharp/

 

Read More

Stack

     

⁉️What is a Stack?

A stack is an abstract data type that follows the Last-In-First-Out (LIFO) principle. In a stack, elements are inserted and removed from only one end, which is known as the top of the stack.

👍Advantages of Stack:

1. Easy to implement and use.
2. Efficient memory management.
3. Supports backtracking in algorithms and programming languages.
4. Provides a simple and organized way to manage and store data.

👎Disadvantages of Stack:

1. Limited functionality compared to other data structures.
2. Size limitations due to finite memory.
3. Can lead to stack overflow errors if too many elements are added.

📌Use Cases:

1. Expression evaluation in programming languages.
2. Backtracking in algorithms.
3. Managing function calls and recursion in programming.
4. Memory management in operating systems.
5. Web browser history management.

🖊️Summary:

A stack is a Last-In-First-Out (LIFO) data structure that allows insertion and deletion of elements from only one end, known as the top of the stack. Stacks are easy to implement and use, provide efficient memory management, and are useful for backtracking in algorithms and programming languages. However, they have limited functionality compared to other data structures, size limitations due to finite memory, and can lead to stack overflow errors if too many elements are added.

📖References:

• https://en.wikipedia.org/wiki/Stack_(abstract_data_type)
• https://www.tutorialspoint.com/data_structures_algorithms/stack_algorithm.htm
• https://www.geeksforgeeks.org/introduction-to-stack-data-structure/
• https://www.programiz.com/dsa/stack

Read More

Queue

 

⁉️What is Queue? 

   A Queue is a data structure that stores elements in a First-In-First-Out (FIFO) order.

 In a queue, elements are added from the back, known as the "enqueue" operation, and removed from the front, known as the "dequeue" operation. 

Queues are used to model scenarios where the order of processing elements matters, such as in scheduling tasks or handling requests.

👍Advantages of Queue:

• Provides a simple and effective way of managing elements in a sequential manner.
• Allows easy addition of elements to the back of the queue.
• Enables easy removal of elements from the front of the queue.
• Provides a predictable behavior in terms of element ordering.

👎Disadvantages of Queue:

• Queues can have a fixed size, which can lead to issues if the number of elements exceeds this size.
• The time complexity of certain operations, such as searching for an element, can be slow.

📌Use Cases:

• Queues are used in operating systems to manage the order in which processes are executed.
• Queues are used in networking to manage the order in which packets are transmitted.
• Queues are used in web servers to handle incoming requests and allocate resources to them.
• Queues are used in printers to manage the order in which print jobs are executed.

🖊️Summary:

A queue is a data structure that allows for elements to be added to the back and removed from the front in a First-In-First-Out (FIFO) order. It provides a simple and effective way of managing elements in a sequential manner, making it useful in a wide range of applications.

 📖References: 

• https://en.wikipedia.org/wiki/Queue_(abstract_data_type)
• https://www.geeksforgeeks.org/queue-data-structure/
• https://www.tutorialspoint.com/data_structures_algorithms/dsa_queue.htm
• https://www.codecademy.com/articles/what-is-a-queue
• https://flaviocopes.com/javascript-data-structures-queue/

 

Read More

Double Linked List

 

⁉️What is Linked List? 

   Double linked list is a data structure in which each node has two pointers, one pointing to the previous node and another to the next node. This allows for bidirectional traversal of the list, making it easier to access and manipulate data.

👍Advantages of Linked Lists:

• Bidirectional traversal allows for more efficient searching, sorting, and manipulation of data.
• Insertion and deletion operations can be performed without needing to iterate through the entire list.
• The list can be traversed in both forward and backward directions.

👎Disadvantages of Linked Lists:

• Double linked lists use more memory than singly linked lists because each node has two pointers instead of one.
• There is an additional overhead cost in maintaining the two pointers for each node.

📌Use Cases:

• Implementing data structures such as stacks and queues that require efficient insertion and deletion of elements.
• Implementing undo/redo functionality in applications such as text editors.
• Building caching mechanisms for frequently accessed data.

🖊️Summary:

    A double linked list is a variation of the linked list data structure that allows for bidirectional traversal of the list. It has advantages such as efficient searching, sorting, and manipulation of data, as well as the ability to traverse the list in both forward and backward directions. 

    However, it uses more memory and has an overhead cost in maintaining the two pointers for each node. It is useful in a variety of applications such as implementing data structures, undo/redo functionality, and caching mechanisms.

📖References: 

• https://github.com/amejiarosario/doubly-linked-list-js
• https://github.com/montagejs/collections/blob/master/doubly-linked-list.js
• https://www.js-data.io/docs/js-data-3.0/collection#doubly-linked-list

Read More

Linked List

⁉️What is Linked List? 

    A linked list is a data structure where each node contains data and a pointer, and is connected in a single line to store data. 

Each node includes a pointer that points to the next node.

    The pointer that points to the next node contains the address of the next node as its value.

    The pointer variable of each node has the address of the data of the next node as its value, and the address of each pointer variable also exists separately.

    A linked list does not arrange its elements in a physical location based on an index like an array.  

    Instead, it creates nodes and connects them to the next node using a pointer. 

    This allows linked lists to avoid rearranging their structure when inserting or deleting data.

👍Advantages of Linked Lists:

• Easy insertion and deletion of new elements.
• Less complexity in restructuring.

👎Disadvantages of Linked Lists:

• More memory usage compared to arrays.
• Inefficient search for specific elements.

📌Use Cases:

• Implementing dynamic data structures like stacks, queues, and hash tables.
• Maintaining and manipulating large datasets efficiently.
• Implementing memory management systems in programming languages.
• Building graph data structures to represent networks or relationships between objects.
• Implementing operating systems and file systems to manage and organize files and directories.
• Building compilers and interpreters to parse and store program instructions.
• Implementing AI and machine learning algorithms to store and process large amounts of data. 

🖊️Summary:

Linked lists provide several advantages such as constant time insertion and deletion, efficient use of memory, and flexibility in terms of size and structure. 

However, they also have some drawbacks such as slower access times and higher overhead costs for storing and managing pointers. 

Therefore, linked lists are often used in combination with other data structures to optimize their performance for specific applications.  

 

📖References: 

• https://www.geeksforgeeks.org/data-structures/linked-list/
• https://www.tutorialspoint.com/data_structures_algorithms/linked_list_algorithm.htm
• https://cslibrary.stanford.edu/103/LinkedListBasics.pdf
• https://www.khanacademy.org/computing/computer-science/algorithms/linked-lists/a/linked-lists

 

Read More